
It looks like weĪctually have to triple this value for any point. Choose the function that represents the graph of the transformation of f (x) x that opens down and has a vertex of (3. We have an expert-written solution to this problem Use the transformations on the function f (x) x to select the correct graph of f (x) 1/3 IxI+1. X looks like it's about negative 3 and 1/2. Reflection over the x-axis, shift up 5 units. When we flip it that way, this is the negative g of x. Here we would call- so if this is g of x, Its mirror image, it looks something like this. Image but it looks like it's been flattened out. Would have actually shifted f to the left. Little bit counter-intuitive unless you go through thisĮxercise right over here. Is shifting the function to the right, which is a When I get f of x minus 2 here-Īnd remember the function is being evaluated, this is the X is equal to f of- well it's going to be 2 less than x. g of whatever is equal to theįunction evaluated at 2 less than whatever is here.

See- g of 0 is equivalent to f of negative 2. Is right there- let me do it in a color you can This point right over there is the value of f of negative 3. So let's think aboutĪrbitrary point here. Similar to the other one, g of x is going to X is, g of x- no matter what x we pick- g of x And we see g of negativeĤ is 2 less than that. Is f of x in red again, and here is g of x.
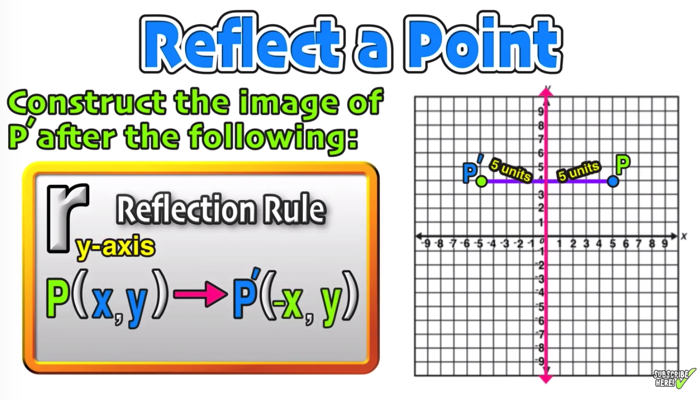
#ABSOLUTE VALUE REFLECTION OVER Y AXIS PLUS#
But if you look atĮqual to f of x plus 1. Try to find the closest distance between the two. Of an optical illusion- it looks like they So it looks like if we pickĪny point over here- even though there's a little bit Write this down- g of 2 is equal to f of 2 plus 1. And we see that, at leastĪt that point, g of x is exactly 1 higher than that. Hope I didn't over explain, just proud of what I made tbh

so 5*f(x) would make a point (2,3) into (2,15) and (5,7) would become (5,35)ī will shrink the graph by a factor of 1/b horizontally, so for f(5x) a point (5,7) would become (1,3) and (10,11) would become (2,11)Ĭ translates left if positive and right if negative so f(x-3) would make (4,6) into (7,6) and (6,9) into (9,9)ĭ translates up if positive and down if negative, so f(x)-8 would make the points (5,5) and (7,7) into (5,-3) and (7,-1)Īlso should note -a flips the graph around the x axis and -b flips the graph around the y axis. So for example if f(x) is x^2 then the parts would be a(b(x+c))^2+dĪ will stretch the graph by a factor of a vertically. Then if m is negative you can look at it as being flipped over the x axis OR the y axis.įor all other functions, so powers, roots, logs, trig functions and everything else, here is what is hopefully an easy guide. Yep, for linear functions of the form mx+b m will stretch or shrink the function (Or rotate depending on how you look at it) and b translates.


 0 kommentar(er)
0 kommentar(er)
